
Do you think Computer Science equals building websites and mobile apps?
Are you feeling that you are doing repetitive and not so intelligent work?
Are you feeling a bit sick about reading manuals and copy-pasting code and keep poking around until it works all day long?
Do you want to understand the soul of Computer Science?
If yes, read SICP!!!
In part 3 we can finally start talking about the digital circuits.
Wire
The wire is an object. It has two states: signal-value and action-procedures.
signal-value represents the current signal on the wire (0 or 1), initialized to 0.
action-proceduresis a collection of procedures to be run when signal changes on the wire.
Constructor
The constructor of wire is implemented using the message-passingstyle. If you don’t know what is message-passing, take a look at my previous post.
(define (make-wire)
(let ((signal-value 0)
(action-procedures '()))
(define (set-my-signal! new-value)
(if (not (= signal-value new-value))
(begin (set! signal-value new-value)
(call-each
action-procedures))
'done))
(define (accept-action-procedure! proc)
(set! action-procedures
(cons proc action-procedures))
(proc))
(define (dispatch m)
(cond ((eq? m 'get-signal)
signal-value)
((eq? m 'set-signal!)
set-my-signal!)
((eq? m 'add-action!)
accept-action-procedure!)
(else (error "Unknown operation:
WIRE" m))))
dispatch))
(define (call-each procedures)
(if (null? procedures)
'done
(begin ((car procedures))
(call-each (cdr procedures)))))
Operations
With the constructor at hand, we can now define the following operations on wires.
(define (get-signal wire)
(wire 'get-signal))
(define (set-signal! wire new-value)
((wire 'set-signal!) new-value))
(define (add-action! wire action-procedure)
((wire 'add-action!) action-procedure))
You can see that these procedures are more of a syntatic sugar. I think they are very self explanatory and need no more words.
Logical Gates
Let’s make gates out of wires.
Inverter
The inverter consisted of two wires, inputand output.
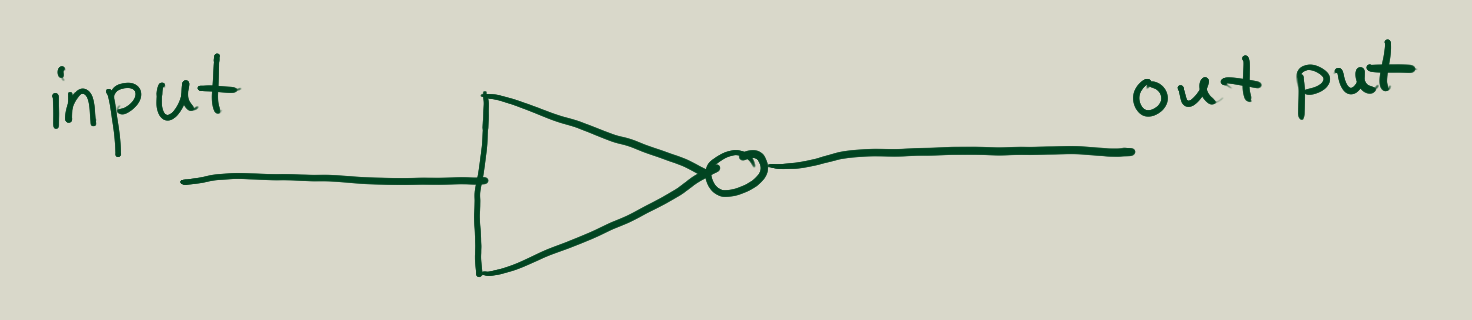
The functionality is to invert signal. But it happens after a delay.
(define (inverter input output)
(define (invert-input)
(let ((new-value
(logical-not (get-signal input))))
(after-delay
inverter-delay
(lambda ()
(set-signal! output new-value)))))
(add-action! input invert-input)
'ok)
(define (logical-not s)
(cond ((= s 0) 1)
((= s 1) 0)
(else (error "Invalid signal" s))))
;; Adds to the global the-agenda an action with a delay
(define (after-delay delay action)
(add-to-agenda!
(+ delay (current-time the-agenda))
action
the-agenda))
(define inverter-delay 2)AND Gate
The AND gate is similar.

(define (and-gate a1 a2 output)
(define (and-action-procedure)
(let ((new-value
(logical-and (get-signal a1)
(get-signal a2))))
(after-delay
and-gate-delay
(lambda ()
(set-signal! output new-value)))))
(add-action! a1 and-action-procedure)
(add-action! a2 and-action-procedure)
'ok)
(define (logical-and a b)
(if (and (= a 1) (= b 1))
1
0))
(define and-gate-delay 3)
OR Gate
Try to implement the OR gate by yourself.
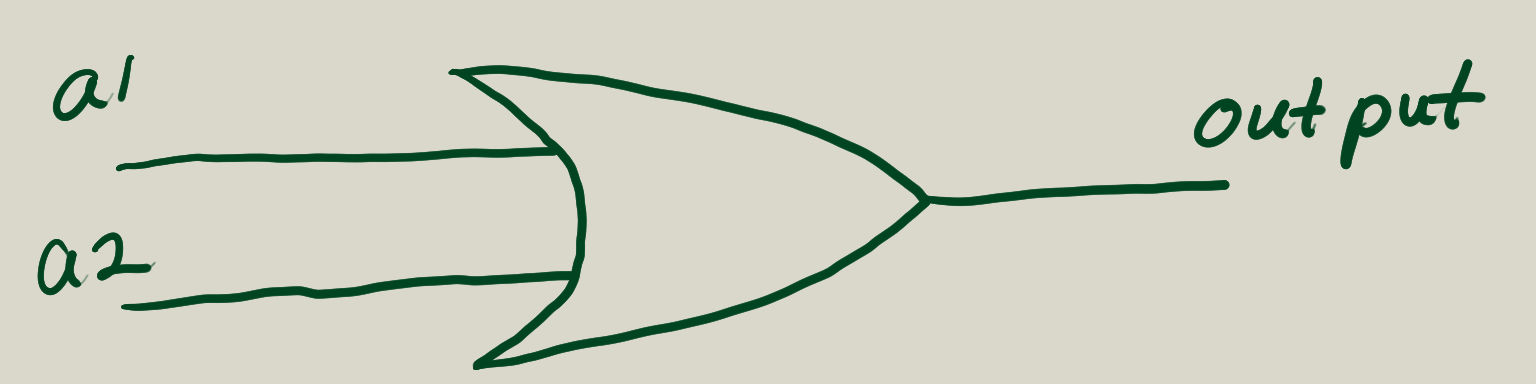
(define (or-gate a1 a2 output)
(define (or-action-procedure)
(let ((new-value
(logical-or (get-signal a1) (get-signal a2))))
(after-delay or-gate-delay
(lambda ()
(set-signal! output new-value)))))
(add-action! a1 or-action-procedure)
(add-action! a2 or-action-procedure)
'ok)
(define (logical-or a b)
(if (and (= a 0) (= b 0))
0
1))
(define or-gate-delay 5)OK, we have implemented everything now. Let’s try to make a real circuit!
Make a simple circuit
Let’s make a circuit as in the following picture:
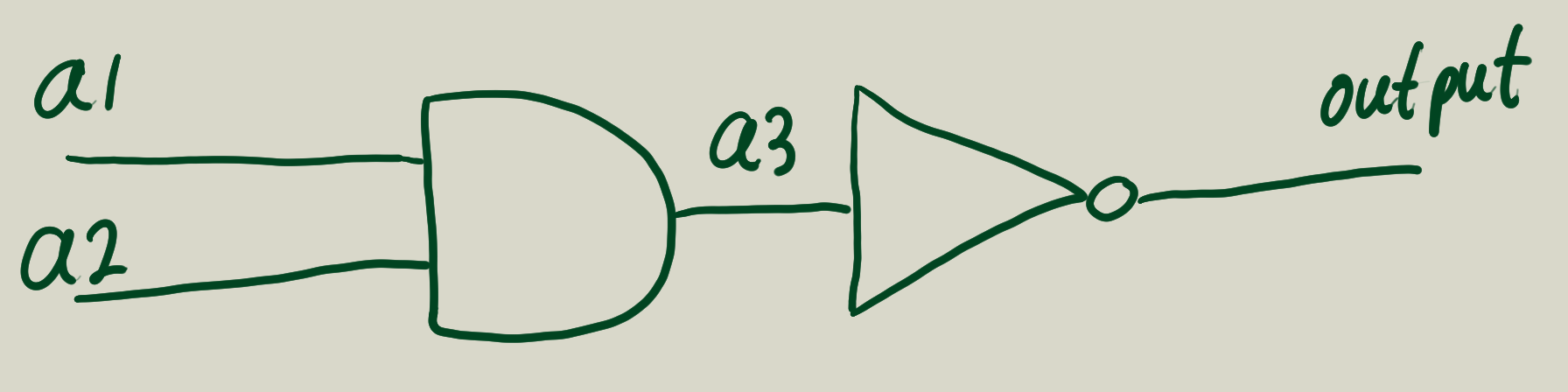
First let’s make a global agenda called the-agenda:
(define the-agenda (make-agenda))Now let’s make the wires and connect them:
; make wires
(define a1 (make-wire))
(define a2 (make-wire))
(define a3 (make-wire))
(define output (make-wire))
;connect the circuit
(and-gate a1 a2 a3)
(inverter a3 output)Let’s pause now, and take a look at the-agenda, what do you think it looks like now? Empty, right? Wrong!
Let’s print the-agenda:
the-agenda
;(0 (2 (#[compound-procedure 14]) #[compound-procedure 14]) (3 (#[compound-procedure 15] #[compound-procedure 16]) #[compound-procedure 16]))It may be a bit hard to make sense of it, but it means:
-
The current simulation time is 0.
-
There are 1 procedure scheduled to run at time 2(#[compound-procedure 14]), and 2 procedures schedulted to run at time 3(#[compound-procedure 15] and #[compound-procedure 16]).
You may wonder, well, we just simply connected the wires and haven’t done anything yet, why there are procedures already scheduled to run in the agenda?
The key is the accept-action-procedure! inside the make-wire procedure:
(define (accept-action-procedure! proc)
(set! action-procedures
(cons proc action-procedures))
(proc))Notice that it execute the new proc right after it put it in the action-procedureslist.
In order to understand why it does it, let’s compare what we get if it does not do it.
Let’s run everything again with the (proc) removed.
Then if we check the-agenda again, it shows:
the-agenda
;(0)Which one do you think is correct?
Let’s judge using common sense.
One thing to note is that all wires have signal 0 by default. Imagine in real life you assembled a circuit just like this, what will happen right after everything is connected?
a1 and a2 both are 0 now, that means and-gate-delay time later, a3 will become 0. Notice also that a3 is already 0 now, that means inverter-delay time later, output will be 1.
Now you should see that even without changing any signal in the circuit, after construction, the circuit will start running automatically, because all the wires have initial signal 0.
OK, now we set the a1’s signal to 1 and call propagate.
(set-signal! a1 1)
(propagate)
the-agenda
; (3)Next we set the a2 also to 1 and propagate.
(set-signal! a2 1)
(propagate)
the-agenda
; (8)Try to go through what really happened and see if you really understand what is going on.

Twitter
Google+
Facebook
Reddit
LinkedIn
StumbleUpon
Email